This is Part I of collaboration series with Professor Isaac Kim, Assistant Professor of Computer Science at UC Davis [Part II here].
(1) Introduction: The Quantum Threat and Opportunity
(1.1) Brief Overview of Quantum Computing
(1.2) The Intersection with Blockchain
(2) Quantum Computing: A Primer for Blockchain Enthusiasts
(2.1) Technical Foundations
(2.2) Current State of Quantum Hardware
(3) Quantum Resistance: Is Crypto Safe?
(3.1) Understanding the Quantum Threat
(3.2) How to Break ECC: Reliable Quantum Computer
(3.3) Building a Reliable Quantum Computer: Quantum Error Correction
(3.4) Advent of Quantum Threat
(3.5) Quantum-Resistant Solutions
(3.6) How to Prepare for the Quantum Threat
(4) Quantum Opportunities for Web3
(5) Final Word
(6) Appendix: Definitions
Summary
Quantum computing is not an immediate threat to crypto, but progress is accelerating. While quantum hardware remains far from breaking today’s encryption, rapid advances in error correction and logical qubit scaling make the long-term threat credible. Blockchain systems dependent on elliptic curve cryptography (ECC) must anticipate a future where key recovery is feasible.
Post-quantum cryptographic (PQC) solutions exist, but adoption is limited by real-world constraints. Although NIST-approved and quantum-resistant schemes offer protection, they often introduce significant overhead in key size, speed, and usability. Only a small subset of blockchains have begun integrating PQC, leaving major protocols like Bitcoin and Ethereum exposed.
Preparation should start before the threat materialises. The emergence of intermediate-scale error-corrected quantum computers (ISEQ) will be the clearest signal that scalable quantum attacks are near. Proactive upgrades — even if inefficient at first — are safer than reactive defenses after a breakthrough.
1. Introduction: The Quantum Threat and Opportunity
Relevant Terms in §1 (full definitions in the appendix):
Qubit: A qubit is the basic unit of quantum information, capable of existing in a superposition of 0 and 1 states simultaneously.
Error Correction: Error correction in quantum computing involves techniques to detect and fix errors in qubit states without directly measuring them, preserving quantum information.
Coherence Time: Coherence time is the duration a qubit can maintain its quantum state before environmental interference causes it to decohere.
Shor's Algorithm: Shor’s algorithm is a quantum algorithm that efficiently factors large integers, posing a threat to classical encryption methods like RSA.
Elliptic Curve Cryptography (ECC): ECC is a public-key cryptography system based on the algebraic structure of elliptic curves over finite fields, offering strong security with smaller key sizes.
Ions: In quantum computing, ions are electrically charged atoms used as qubits in ion trap quantum computers due to their long coherence times and precise control.
The intersection of quantum computing and blockchain technology presents one of the most fascinating dichotomies in modern technology: a potential existential threat that simultaneously offers remarkable opportunities. As 2025 unfolds, understanding this dynamic relationship requires a pragmatic lens, free from both the hyperbole that often surrounds quantum computing and the dismissive attitudes occasionally found in crypto circles.
1.1 Brief Overview of Quantum Computing
The current state of quantum computing differs markedly from popular media narratives. Industry data indicates that major players like IBM and Google are making steady, albeit measured progress. IBM's recent 1,000+ qubit system, whilst impressive, still faces significant challenges in error correction and coherence time.
Concepts in quantum computing lie in a fundamentally different computational paradigm to those found in classical computing (Figure 1). The key distinctions lay in quantum computing’s ability to perform certain calculations exponentially faster than classical computers can, and it is this capability which holds profound implications for cryptographic systems.
Figure 1: Quantum Computers Differ from Classical Computers in Many Ways

Source: Presto Research
1.2 The Intersection with Blockchain
The relationship between quantum computing and blockchain technology reveals particularly nuanced dynamics. While considerable attention has focused on quantum computing's threat to cryptographic systems, this narrative oversimplifies a complex reality. Most blockchain protocols rely on elliptic curve cryptography (ECC) - a form of public-key cryptography that secures digital assets by leveraging the mathematical difficulty of the elliptic curve discrete logarithm problem. This ensures that even if a public key is widely visible, deriving the corresponding private key remains computationally infeasible using classical methods.
However, this foundation does not hold in a quantum context. Shor’s algorithm, a quantum algorithm developed in the 1990s, can efficiently solve both integer factorisation and discrete logarithm problems including the elliptic curve variant used in ECC. In principle, a sufficiently large and reliable quantum computer running Shor’s algorithm could compromise ECC-based systems by recovering private keys from exposed public keys. Figure 2 shows how quantum computers running Shor’s algorithm can extract a private key from an exposed public key. Wallets remain secure as long as the public key remains hashed, but become vulnerable at the point of exposure, either during transaction broadcasting or in legacy wallet formats where public keys are already visible.
Figure 2: Quantum Attack Path on ECC-Based Wallets.
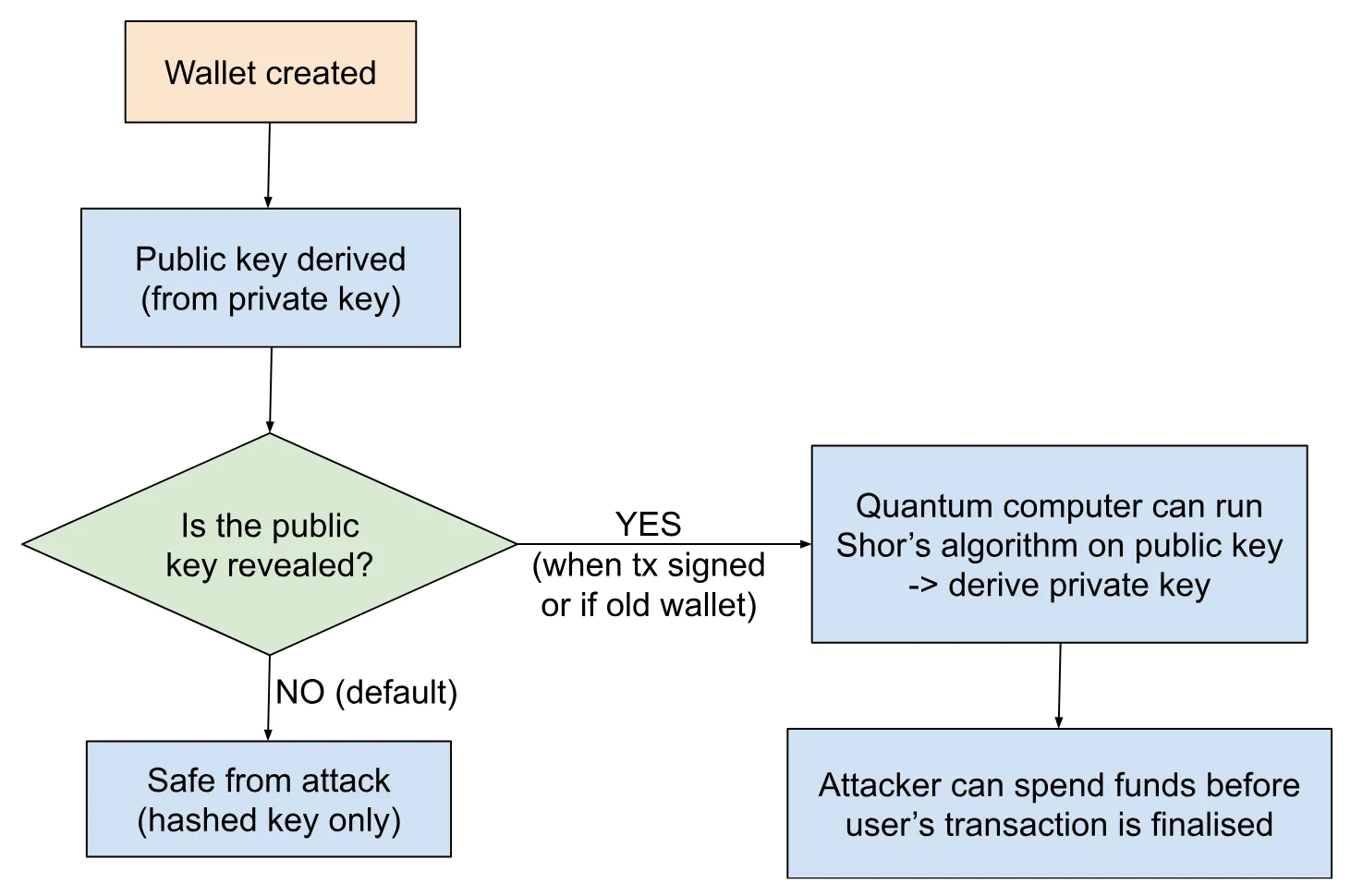
Source: Presto Research
The technical requirements for implementing such attacks at a meaningful scale remain substantially beyond current capabilities. Nevertheless, the mere existence of this vulnerability has catalysed notable innovation in the blockchain space. Several projects have begun implementing post-quantum cryptography (PQC) schemes, reflecting a maturing industry that considers decades-ahead scenarios rather than merely reacting to immediate challenges.
The financial stakes are significant. As of April 2025, blockchain networks secure almost $3 trillion in assets through cryptographic systems that could theoretically face vulnerability to quantum attacks. This has created an environment where the possibility of future quantum capabilities drives present-day innovation and investment in blockchain security.
The challenges for the industry are both technical and strategic as it will need to simultaneously build systems today that will remain secure in a post-quantum world, and position it to leverage quantum advantages when they become available. There is no single prescription and consequently this report will instead focus on the dual challenge ahead: safeguarding existing infrastructure whilst exploring what quantum-native innovation might look like.
2. Quantum Computing: A Primer for Blockchain Enthusiasts
Relevant Terms in §2 (full definitions in the appendix):
Superconducting: Superconducting refers to materials that conduct electricity with zero resistance at very low temperatures, commonly used to build qubits in gate-based quantum computers.
Fault Tolerance: Fault tolerance in quantum computing is the ability of a system to continue correct operation despite the presence of errors or qubit failures.
Quantum: Quantum relates to the discrete, probabilistic nature of phenomena at atomic and subatomic scales, foundational to quantum computing and cryptography.
Superposition: Superposition is a quantum property allowing a qubit to exist in multiple states simultaneously, unlike classical bits.
Entanglement: Entanglement is a quantum phenomenon where particles become correlated such that the state of one instantly influences the other, regardless of distance.
Interference: Interference in quantum systems occurs when probability amplitudes combine, either reinforcing or cancelling out outcomes, critical to algorithmic success.
Gate-Based Quantum Computing: Gate-based quantum computing uses sequences of quantum logic gates to manipulate qubits and perform computations.
Quantum Annealing: Quantum annealing is a computational method using quantum fluctuations to solve optimisation problems by finding low-energy states.
Quantum Fourier Transform: The Quantum Fourier Transform is a linear transformation on qubits, used in algorithms like Shor’s for period finding and factorisation.
Grover's Algorithm: Grover’s algorithm is a quantum search method that provides a quadratic speedup for unstructured search problems.
Logical Qubit: A logical qubit is a stable, error-corrected unit of quantum information composed of multiple physical qubits.
Measurement Collapse: Measurement collapse is the process where a qubit's superposition resolves into a definite classical state upon observation.
Qubit Decoherence: Qubit decoherence refers to the loss of quantum information due to interaction with the environment, leading to classical behaviour.
Trapped Ions: Trapped ions are qubits made from ions confined and manipulated using electromagnetic fields in vacuum chambers.
Topological Qubits: Topological qubits use quasiparticles that store information non-locally, offering inherent resistance to local noise and decoherence.
Quantum Data Plane: The quantum data plane handles the physical execution of quantum operations, including qubit manipulation and entanglement.
Quantum Control Plane: The quantum control plane coordinates the scheduling, synchronisation, and pulse control of qubits during computations.
Host Processor: The host processor is the classical computer that interfaces with the quantum processor, orchestrating instruction flow and data processing.
Neutral Atoms: Neutral atoms are uncharged atoms used as qubits, held in place by optical tweezers and offering scalability for quantum computing.
Photons / Photonic Qubits: Photonic qubits are quantum bits encoded in particles of light, valued for their speed and low interaction with the environment.
2.1 Technical Foundations
Quantum computing represents a fundamental shift in computational paradigms. While classical computers operate on bits (0s and 1s), quantum computers utilise qubits. The significance extends beyond multiple states - it lies in how these states can be manipulated to solve specific types of problems exponentially faster than classical computers.
The practical implications for blockchain focus on mathematical problems underlying cryptographic security, which become significantly easier to solve with quantum computers. These speed-ups are mathematically provable rather than theoretical.
Core Quantum Principles
Understanding the intersection of quantum computing and blockchain requires familiarity with several foundational quantum mechanics principles:
Superposition: Unlike classical bits that exist in a definite state of either 0 or 1, qubits can exist in multiple states simultaneously. This feature, together with interference, endows quantum computers with computational capabilities beyond classical computers.
Entanglement: This uniquely quantum phenomenon allows multiple qubits to become correlated in a form that cannot be mimicked classically. Einstein famously referred to this as "spooky action at a distance." Entanglement enables quantum systems to create complex, correlated states that can be leveraged for computational advantage.
Interference: Quantum algorithms leverage interference to amplify probability towards correct answers while diminishing incorrect ones. This manipulation of probability amplitudes allows quantum computers to converge efficiently on solutions to certain problems, creating algorithmic speedups.
Quantum Computing Models
Several computational models have emerged to harness quantum properties:
Gate-Based Quantum Computing: Similar to classical computing's logic gates, quantum gates manipulate qubits in a circuit-like model. This is the most general approach and powers many of the theoretical quantum algorithms relevant to cryptography. IBM, Google, and others are pursuing this model.
Quantum Annealing: A specialised approach optimised for solving specific optimisation problems by finding minimum energy states. D-Wave's systems use this approach, which offers potential advantages for certain classes of problems but is less applicable to cryptographic challenges. In a gate-based model, Shor’s algorithm can solve problems relevant to cryptography. However, for the same problem only heuristic methods exist in quantum annealing, with very little evidence showing that it can solve large-scale problems.
Key Quantum Algorithms
Several quantum algorithms have been developed that demonstrate quantum advantage for specific problems:
Shor's Algorithm: Developed by Peter Shor in 1994, this algorithm efficiently factors large integers and computes discrete logarithms. It demonstrates an exponential speedup over the best-known classical algorithms for these problems.
Grover's Algorithm: Provides a quadratic speedup for unstructured search problems, effectively searching an unsorted database of N items in approximately √N steps instead of the classical N steps.
Quantum Fourier Transform: A quantum version of the classical Fourier transform that forms the basis of many quantum algorithms, including Shor's. It can be implemented exponentially more efficiently on a quantum computer than its classical counterpart.
Quantum Computing Measurement
One critical aspect of quantum computing is measurement. When measured, qubits collapse from their superposition state to a classical state (either 0 or 1). This probabilistic nature of quantum measurement means quantum algorithms must be cleverly designed to increase the probability of measuring the desired result.
2.2 Current State of Quantum Hardware
There are multiple essential hardware layers that collaborate into making quantum computing possible:
The Quantum Data Plane: This houses the physical qubits and their support structures in isolation, and contains a programmable “wiring” network for multi-qubit operations.
The Control and Measurement Plane: This converts digital instructions into precise analog signals to manipulate qubits, while also handling measurements. It requires extensive calibration and careful signal isolation to prevent crosstalk between qubits.
The Control Processor Plane: This orchestrates the quantum operations in real-time, processing both the quantum algorithm requirements and error correction data. It needs to operate with sufficient speed to keep pace with quantum operations.
The Host Processor: This is a classical computer that provides the user interface, program control, and data management. It connects to the control processor through high-bandwidth links.
Figure 3: Interior of an IBM Quantum System One model.

Source: IBM Research [link]
Current hardware implementations are primarily focused on the following approaches:
Superconducting Qubits: These are fabricated using lithographic circuits that operate at near-absolute zero temperatures. They offer fast operation times in the nanosecond range and leverage existing semiconductor manufacturing techniques. IBM and Google dominate this approach, with IBM's 127-qubit Eagle processor and Google's Sycamore demonstrating the current state of this technology. Current systems demonstrate around 70 qubits, with an expected scaling limit of about 1000 qubits using present methods. Their main scaling constraints stem from wiring complexity, control electronics, cooling requirements, and establishing coherent quantum connection between different superconducting chips.
Trapped Ions: These use individual ions as qubits, controlled by laser systems within vacuum chambers. While they operate more slowly (microseconds rather than nanoseconds), they provide excellent connectivity between qubits. Quantinuum leads in technology, with systems like H2 (56 qubits). Their scaling limitations primarily relate to trap size management and photonic interconnects.
Topological Qubits: Microsoft has invested heavily in this approach, recently claiming a breakthrough with their Majorana 1 chip. This approach offers inherent stability against decoherence by using a novel state of matter in principle. However, these claims remain controversial within the scientific community, with some researchers demanding more evidence before accepting the validity of Microsoft's announcements.
Quantum Annealing: D-Wave specialises in this approach, using superconducting qubits arranged for optimisation problems. Their Advantage system boasts over 5,000 qubits but operates differently from the "gate-based" quantum computers developed by other players. Whether this approach can solve some problems faster than classical computers remains controversial.
Neutral Atom: These use individual atoms instead of ions, trapped by optical tweezers. There are three companies who are based on this technology (Atom Computing, Pascal, QuEra) This is a new emerging approach that can potentially scale up to tens of thousands of qubits in a single trap. In particular, 256 qubit machines by Atom Computing and QuEra were announced. While promising, the existing machines have not demonstrated the necessary requirements for building a large-scale quantum computer in a single system, such as mid-circuit measurement and feedback.
Photon: These use photons as qubits, primarily pursued by PsiQuantum and Xanadu. This technology had struggled to produce reliable qubits, but they were pursued primarily because of their scaling advantage.
While the field faces several critical hardware challenges, near-term hardware developments suggest we'll see systems with 50-100 qubits, though error rates remain too high for effective error correction. The primary limitations include:
Qubit Stability: Qubits are extremely sensitive to environmental noise, quickly losing their quantum state through decoherence. This fundamental challenge is particularly relevant for crypto, as breaking encryption requires maintaining quantum states long enough to run complex factoring algorithms.
Scalability: Building systems with thousands or millions of qubits while maintaining reliability presents enormous challenges. No clear path exists yet for creating the large-scale fault-tolerant quantum computers that would pose a threat to blockchain security.
Error Correction: Quantum computations are inherently error-prone, with practical quantum error correction requiring multiple physical qubits to create a single reliable "logical qubit." This significantly increases hardware requirements.
Cooling Requirements: Superconducting systems require operation near absolute zero, necessitating expensive cryogenic infrastructure that adds considerable cost and practical limitations.
Control and Measurement: Precisely managing and measuring quantum states becomes increasingly challenging as systems grow, requiring sophisticated electronics and calibration processes.
For crypto natives concerned about quantum threats to blockchain security, the current hardware reality offers considerable reassurance. While quantum computing is advancing steadily, the gap between today's capabilities and what's needed to break cryptographic systems remains vast. The industry continues to pursue multiple hardware approaches in parallel, recognising that different technologies may prove optimal for different applications.
3. Quantum Resistance: Is Crypto Safe?
Relevant Terms in §3 (full definitions in the appendix):
Public-Key Cryptography: Public-key cryptography is an encryption method where two distinct keys—one public and one private—are used for secure data exchange and digital signatures.
RSA: RSA is a widely used public-key cryptographic system based on the computational difficulty of factoring large composite integers.
Discrete Logarithm: The discrete logarithm problem involves finding an exponent in modular arithmetic and underpins the security of several cryptographic systems, including ECC.
Hashed Public Key: A hashed public key is the output of applying a cryptographic hash function to a public key, often used to enhance privacy or compress key representation in blockchains.
Quantum Error Correction: Quantum error correction refers to methods for protecting quantum information by encoding it in multiple physical qubits to detect and correct errors without direct measurement.
Physical Qubit: A physical qubit is a single, hardware-level qubit that stores quantum information but is often prone to errors and instability.
Logical Error Rate: The logical error rate is the effective error rate observed in an error-corrected logical qubit, reflecting how well quantum error correction is working.
ISEQ (Intermediate-Scale Error-Corrected Quantum Computer): ISEQ denotes a class of near-term quantum devices that implement error correction and support meaningful algorithms without yet reaching full fault tolerance.
DARPA QBI / US2QC: DARPA QBI (Quantum Benchmarking Initiative) and US2QC (Underexplored Systems for Utility-Scale Quantum Computing) are US government research programmes aimed at evaluating and accelerating advanced quantum architectures.
Post-Quantum Cryptography (PQC): Post-quantum cryptography encompasses cryptographic algorithms designed to be secure against attacks by quantum computers, replacing vulnerable classical schemes like RSA and ECC.
One-Time Signature (OTS): A one-time signature is a cryptographic signature scheme intended for secure use in only a single message signing, often used in hash-based post-quantum systems.
Lamport Signatures: Lamport signatures are a type of one-time signature based on one-way functions and considered a foundation of post-quantum secure signing.
Winternitz Scheme: The Winternitz scheme is an enhancement of Lamport signatures that improves signing efficiency by reducing key and signature size through limited multiple-use hash chains.
3.1 Understanding the Quantum Threat
The security of blockchain technology relies on the public-key cryptosystem. In a public-key cryptosystem, there is a public key, which is available to everyone, and a private key, which is only available to the rightful user. Obtaining the private key from the public key is possible in principle, but the computational cost is exorbitant. For instance, in the RSA (Rivest-Shamir-Adelman) cryptosystem, the private key is a pair of integers, and the public key is the two numbers multiplied. Verifying that somebody has the correct private key is easy, because you can easily multiply two numbers. But, obtaining the private key entails performing prime factorization, a task that is known to be extremely challenging. This computational difficulty is what ensures the security of the RSA cryptosystem.
In 1994, Peter Shor famously showed that quantum computers can factor large integers efficiently. If we have a large enough quantum computer, we can easily obtain private keys of the RSA cryptosystem from its public keys, making this scheme vulnerable to quantum attacks. In fact, a simple variant of Shor’s algorithm can be used to break nearly all the known public-key cryptosystems used in blockchains, which are based on the elliptic curve cryptography (ECC).
Does this mean that quantum computers will wipe out the blockchain ecosystem as we know it? In the short term, the answer is likely no. This is for a simple reason that the quantum computers that are expected to be available over the next few years will be not powerful enough to run Shor’s algorithm at scale. Moreover, modern blockchain wallets have an extra layer of security, using cryptographic hash functions like SHA-256. Instead of revealing the public keys, what is being revealed is a hashed public key. Although quantum computers can efficiently recover the private key from the public key, they cannot from the hashed public key. Therefore, for most modern wallets, there is likely no near-term quantum threat.
Figure 4: Elliptic curves have interesting properties
Source: Presto Research
However, as progress in quantum computing continues, there will be a point at which various vulnerabilities will arise. Although the public key is hashed, they must be revealed when a transaction occurs. When a transaction is broadcast to the blockchain network, the public key can be already visible to everyone. Therefore, an adversary with a quantum computer can recover the private key, which can be used to steal the funds stored in the wallet before the transaction occurs. This line of attack shows that simply hashing the public key is not enough. If quantum computers become large and fast enough to recover the private key before the transaction finishes, hashed keys by themselves will no longer be a solution against quantum attacks.
In fact, public keys can be revealed through other mechanisms as well. Although modern wallets discard the public key after the transaction occurs, older ones did not. For instance, some of the old Bitcoin P2PKH addresses are revealed already, and they will be extremely vulnerable to the quantum attack. In Ethereum, the public key is tied to the account, and as such, there is more danger of the public key being revealed.
To summarize, quantum computers that will be available in the next few years will not be powerful enough to pose a threat to the integrity of blockchain technology. However, in the long term, many of the existing blockchain protocols may become vulnerable to quantum attacks. At some point, a change must be made to protect the blockchain assets from these vulnerabilities.
3.2 How to Break ECC: Reliable Quantum Computer
Quantum computers will pose a threat to blockchain technology eventually, but when exactly? Predicting the exact timeline is challenging because quantum computing is a nascent field; progress in algorithm, hardware, and architecture is being made at a rapid pace, and it is difficult for the non-experts to assess which are genuine progress or not.
The good news is that there is a consensus on what kind of quantum computer is needed to break the ECC used in blockchains. To do so, it is currently estimated that one needs to apply 10^7-10^8 quantum gates, on thousands of qubits. Although building a quantum computer consisting of thousands of qubits is already possible these days, the existing quantum computers are not reliable enough. Each gate applied is susceptible to an unwanted noise, and even a single noise has a potential to render the outcome of the computation useless. In order to break ECC, we need to ensure that almost no error occurs while applying the 10^7-10^8 quantum gates.
To ensure that level of reliability, each gate should have an error rate of no larger than 10^8 (more conservatively, in the 10^(-11)-10^(-10) range). This is significantly lower than what is currently achievable. The current best error rate hovers at around 10^(-3). Bridging this gap between these two vastly different numbers is the primary challenge needed to breaking the ECC.
3.3 Building a Reliable Quantum Computer: Quantum Error Correction
Although the gap between the currently achievable error rate (10^(-3)) and what is needed to break ECC (10^(-8)-10^(-11)) may seem large, this is not necessarily the case. To understand why, it is important to understand the mechanism by which the quantum computing practitioners intend to lower the error rate in the future: quantum error correction.
Quantum error correction, as the name suggests, is a method to correct an error occurring in a quantum computer. Quantum error correction started off as a theoretical subject, and it led to the following two important predictions. Provided that the physically achievable error rate is low enough (~10^(-3)), the following is possible.
By encoding quantum information in many qubits, one can reduce the error rate.
As the number of qubits increases, the error rate decreases exponentially.
If true, these predictions are significant for the following reason. Because the error rate would decrease exponentially, even adding a small extra number of extra qubits will reduce the error rate by an order of magnitude. In particular, even though the gap between the currently achievable error rate (10^(-3)) and the error rate needed to break ECC (10^(-8)-10^(-11)) may seem large, the number of extra qubits needed to reduce the error rate to the desired level would be modest. It is currently estimated that the number of additional qubits to get one very reliable qubit is anywhere between 50 to a few hundred, depending on various assumptions.
3.4 Advent of Quantum Threat
Recently, there has been rapid progress in quantum error correction. In particular, some companies (Quantinuum, Google) have demonstrated the theoretical prediction that the error rate can be reduced by encoding quantum information in many qubits. More recently, Google demonstrated that as the number of qubits increases, the error rate decreases exponentially as expected (Figure 5). So at this point, all the basic principles of quantum error correction have been demonstrated, leaving little doubt that it works.
Figure 5: Google’s 105-qubit Willow processor surface code performance.
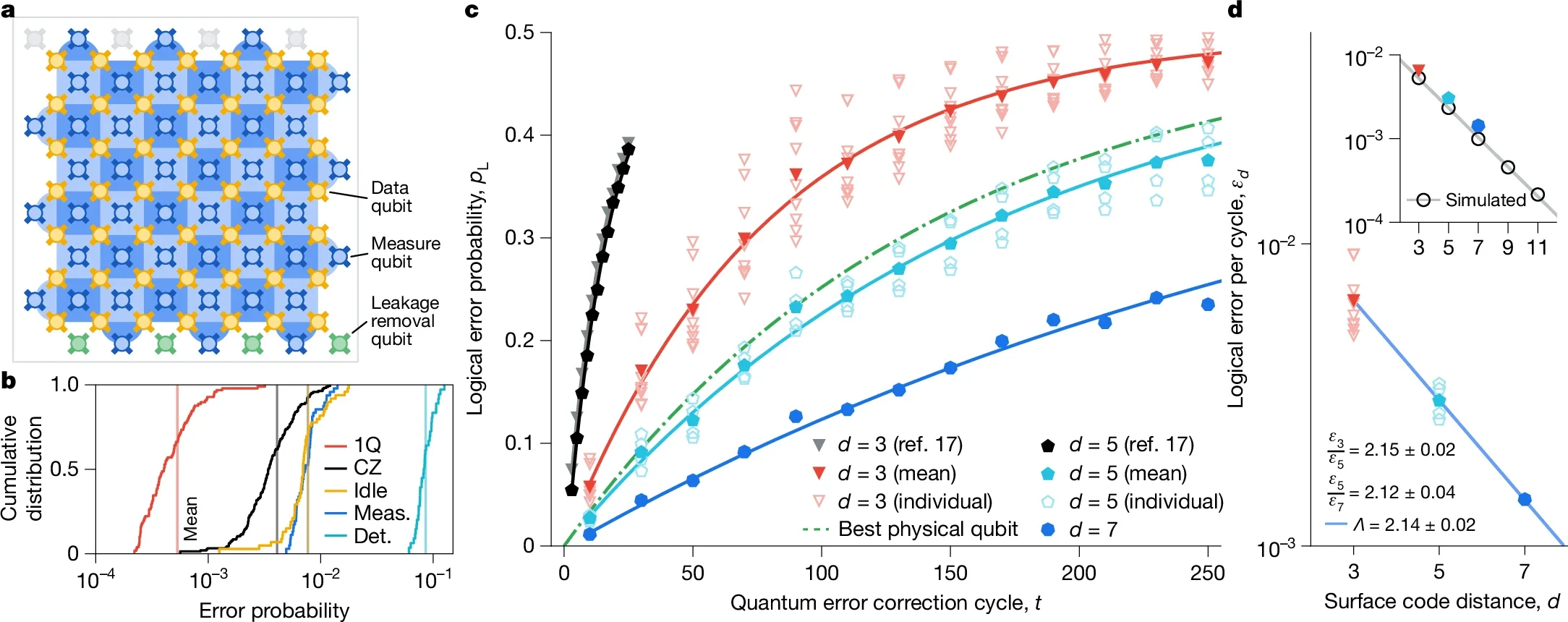
Source: Google Quantum AI and Collaborators
Because the error rate decreases exponentially with the number of qubits, the reduction in error rate will be sudden and not gradual. Therefore, even though progress in quantum computing may seem slow currently, the rate of progress will be more rapid in the future. Even if the number of qubits grows linearly in time, the error rate will decrease exponentially. If we expect the number of qubits to grow exponentially in time (like Moore’s law), the error rate will decrease at an even more rapid pace.
When it comes down to assessing the quantum threat, the real question is if there is any technology capable of maintaining an error rate of 10^(-3) or lower that can be also scaled up easily. If there is even a single company that can achieve such a feat, the integrity of the blockchain technology will be seriously compromised.
The trouble is that there are many quantum computing companies with different technologies and approaches. Recently, DARPA announced the Quantum Benchmarking Initiative (QBI) program, whose goal is to build a quantum computer capable of solving useful problems. We expect any company that is capable of passing DARPA’s stringent requirement to be also able to break ECC. There are currently 15 companies in this list, and there is also a related program from DARPA called Utility-Scale Quantum Computing (US2QC), which includes two additional companies (Microsoft and PsiQuantum). That amounts to 17 quantum computing companies spanning various complementary approaches, all aimed at building a large-scale quantum computer. Even if one thinks that the probability of each succeeding is about 10%, there is a high probability that at least one of them will succeed, making the blockchain technology vulnerable to quantum attacks in the foreseeable future.
3.5 Quantum-Resistant Solutions
There have been some recent movements to incorporate resistance against quantum attacks. For instance, there are some blockchains that employ post-quantum cryptography (QRL, IOTA, ALGO, CELL, MCM, QANX, to name a few). Some wallets that are resistant to quantum attacks were built for some blockchains, such as for Ethereum or Solana.
Figure 6: The Top 5 Cryptocurrencies Secure Over $2T

Source: Presto Research
At the heart of these projects lie cryptographic schemes that are expected to be resistant to quantum attacks. Some of these are based on one-time signature (OTS) schemes such as Lamport or Witernitz. And the others employ NIST-approved post-quantum cryptography (PQC) schemes, which are all public-key cryptosystems.
These approaches have their own pros and cons. The security of OTS schemes are well-established against quantum attacks. However, they can be inconvenient to use because one cannot use the same key to sign multiple messages. Public-key cryptosystems are easier to use in this regard. However, key generation and authentication tends to be costly for these PQC schemes, making its execution on-chain impractical. Therefore, while these schemes can provide resistance against quantum attacks, their practical implementation poses a challenge.
While the recent incorporation of PQC schemes is encouraging, still the majority of the blockchain technology has not implemented these changes. In particular, the two dominant blockchains (Bitcoin and Ethereum) are still vulnerable to quantum attacks. If a large-scale quantum computer becomes available, any vulnerability of these blockchains can significantly undermine its value. There are current plans to upgrade them with PQC schemes, though we are far from the implementation stage.
One argument against implementing these PQC schemes soon is that large-scale quantum computers are likely multiple decades away. That could be true, but one cannot deny the fact that there are nearly 20 companies with different complementary approaches that are aiming to build a large-scale quantum computer in 10 years, and possibly in a shorter time frame. The possibility of ECC being compromised within this timeframe cannot be completely neglected. What is more, as explained in Section 3.4, as quantum computers scale up, there will be a drastic improvement; we can have a hardly working quantum computer in one year, only to have an extremely reliable quantum computer the year after. Incorporating PQC only after a quantum computer becomes scalable can be risky; once the technology becomes scalable, there simply may not be enough time to safeguard the crypto assets.
3.6 How to Prepare for the Quantum Threat
Predicting exactly when a large-scale quantum computer will be available is difficult. However, the good news is that there are important milestones that need to be achieved along the way, which will likely be announced publicly. By keeping track of which companies are achieving these milestones (or not), one can get an idea on how close we are from breaking ECC.
The key concept that we advocate for this purpose is a notion of intermediate-scale error-corrected quantum computer (ISEQ). This is a quantum computer that is not capable of breaking ECC, yet advanced enough to be of some scientific value. From the blockchain perspective, the advent of ISEQ would be a strong indication that the quantum threat is imminent. Let us break down the events signify the advent of ISEQ and why this would pose a vulnerability of the blockchain technology in a future not too far away.
Figure 7: Quantum Computing Scaling
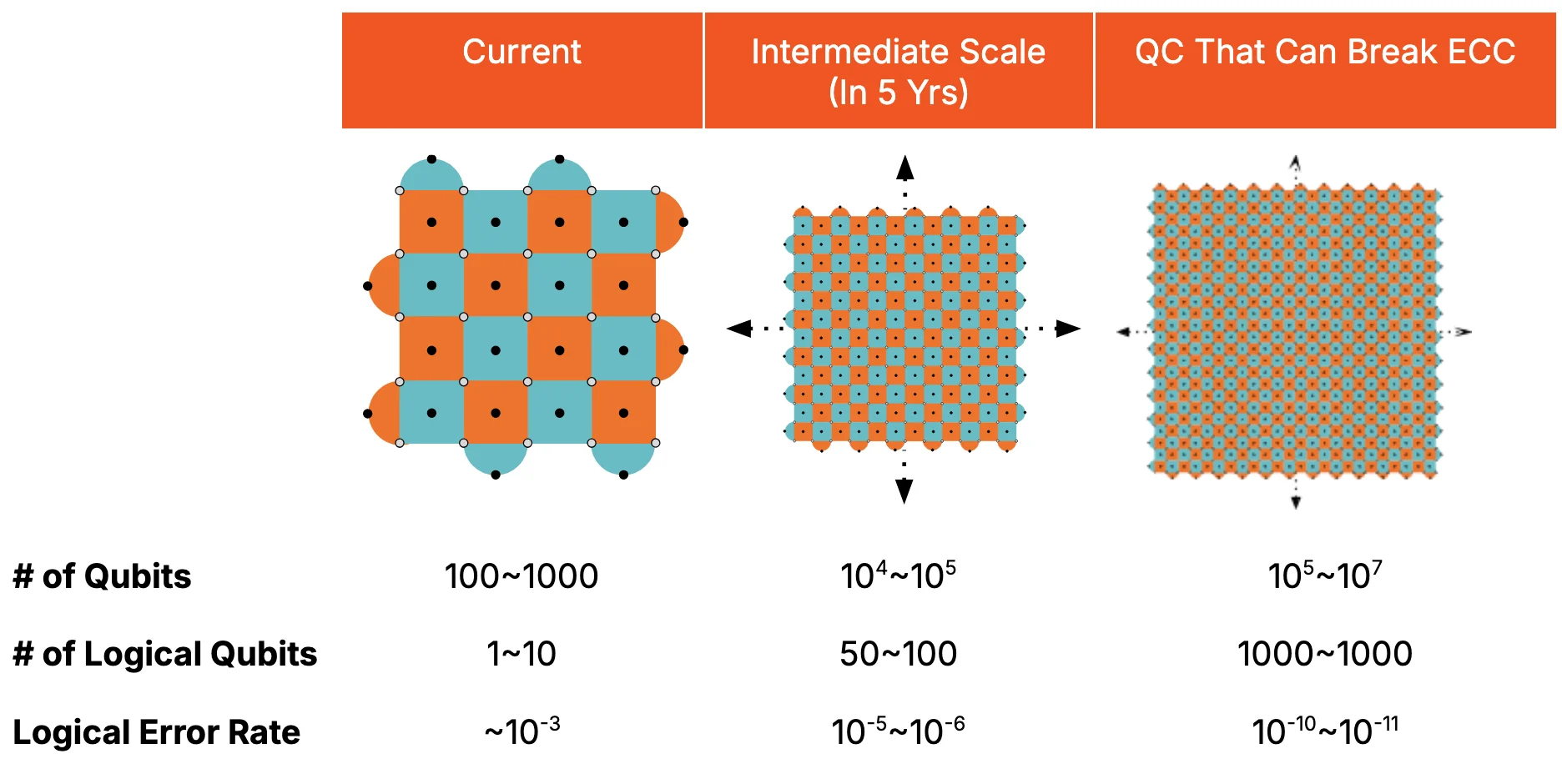
Source: Presto Research
The first notable event would concern the error rate, in particular, achieving a logical error rate of 10^(-5) or lower. To put this into context, some companies (Quantinuum, Google) have already demonstrated that one can bring down the logical error rate below the physical error rate by performing quantum error correction; the expectation is that the logical error rate will continue to drop as the system is scaled up, which Google demonstrated already albeit at a small scale.
One difficulty in keeping track of progress like this is that there are different versions of what people mean by logical error rate, and by twisting the definition, it is possible to make the number look better than what it actually is. This subtlety is difficult to decipher for anyone who is outside of the field. However, achieving a logical error rate of 10^(-5) is currently challenging no matter which version of logical error rate is used. Therefore, achieving this number is expected to be a genuine progress in the field of quantum computing.
There is also another reason why the logical error rate of 10^(-5) is important. Once it becomes possible to achieve an error rate of 10^(-5), suddenly there are a plethora of new options that can suppress the error further. In contrast, at the logical error rate of 10^(-3) (which is currently achievable and similar to the physical error rate), there are significantly fewer options. So in some sense getting to 10^(-10)-10^(-11) error rate from 10^(-5) error rate is significantly easier than getting to 10^(-5) error rate from 10^(-3) error rate, insofar as the same system can be scaled to a larger size.
Lastly, once the logical error rate of 10^(-5) is achieved, some of the scaling challenges in quantum computing will likely be much easier to deal with. For many quantum computing approaches, to eventually build a large-scale quantum computer capable of breaking ECC, some kind of interconnect between different quantum computing modules is necessary. For many approaches (except for photon-based approaches), this interconnect is less reliable and slower than the operations available within each module. Therefore, building a reliable interconnect might be the main bottleneck in building a large-scale quantum computer. However, once a logical error rate of 10^(-5) or lower can be achieved, the demand on the reliability of the interconnect becomes significantly more benign, capable of tolerating more errors on the interconnect.
The second requirement for ISEQ is to scale the number of logical qubits to hundred or more, while maintaining the logical error rate of 10^(-5) or less. This would be a significant development for the following reasons. If one can build a quantum computer with a logical error rate of 10^(-5) consisting of roughly hundred logical qubits, it is possible to reduce the logical error rate within the same system to the requisite 10^(-10)-10^(-11) level, albeit with fewer logical qubits. Therefore, this would be almost exactly the same point at which one can achieve the logical error rate needed to break ECC. Once this is achieved, breaking the ECC will be likely possible by scaling up the system by a factor of 10-100, a large but not an overly ambitious goal.
These two requirements — achieving a logical error rate of 10^(-5) or less and having ~100 logical qubits — may seem still far from the requirement of building a quantum computer capable of breaking the ECC. After all, the latter requires substantially lower logical error rate (10^(-10) - 10^(-11)) and thousands of logical qubits. However, the key point is that any technology that is capable of building ISEQ is likely good enough to build an even larger scale system. The difference between the two systems will not lie in the technology, but rather on the amount of resource needed. Once a quantum computing company proves that their technology works, attracting the necessary investment will be easier, making the advent of larger-scale quantum computers much more imminent.
So, when will ISEQ arrive? The current consensus is that there is a non-negligible chance of this happening within the next five years. Building such a system is certainly well within the public timelines announced by some of the companies (most notably QuEra and PsiQuantum). While it is difficult to predict if any of the companies will build ISEQ in the next five years, the current consensus is that this is a challenging but not an impossible goal. To prepare for the advent of the quantum threat for blockchain technology, one would have to take a closer look at which companies are making progress towards building such a system. In particular, one should pay close attention to any of the companies achieving a logical error rate of 10^(-5) or less. This will be a strong evidence of rapid progress to come in the near future.
Once an ISEQ is built, the rate of progress in quantum computing may accelerate substantially, because of the relative lack of technological bottlenecks and the likely increased amount of investment. To err on the safer side, it will be best to upgrade the protocols used in the existing blockchain technology to the quantum-resistant ones even before the advent of ISEQ.
4. Quantum Opportunities for Web3
Relevant Terms in §4 (full definitions in the appendix):
Supersingular Isogeny: Supersingular isogeny refers to a cryptographic scheme based on the hardness of finding isogenies (special algebraic maps) between supersingular elliptic curves, forming the basis of certain post-quantum protocols.
Side-Channel Attack: A side-channel attack exploits indirect information—such as timing, power usage, or electromagnetic emissions—from a cryptographic device to extract secret keys or sensitive data.
Zero-Knowledge Proofs (ZKP): Zero-knowledge proofs are cryptographic methods that allow one party to prove knowledge of a statement's truth to another without revealing the underlying information.
Quantum Random Beacons: Quantum random beacons generate publicly verifiable, unpredictable random numbers using quantum processes, useful for cryptographic protocols and consensus mechanisms.
Quantum-Enhanced MPC: Quantum-enhanced multi-party computation (MPC) refers to secure collaborative computation protocols that leverage quantum properties to increase privacy, correctness, or performance guarantees.
The largest quantum opportunity for Web3 by far lies in its protection against future quantum attacks, which entails upgrading the existing infrastructure to be quantum-resistant. While such an upgrade is inevitable eventually, there are practical challenges that make this transition difficult.
The first major challenge is that the security of the PQC schemes are not yet tested rigorously in the real world, at least compared to the widely used cryptosystems like RSA and ECC. In fact, one of the PQC schemes initially proposed was shown to be vulnerable even against quantum attacks. Moreover, one of the NIST-approved PQC schemes was shown to be vulnerable against a side-channel attack.
To be clear, these events on their own do not imply that all PQC schemes are insecure. There are NIST-approved PQC schemes which so far remain unbroken, and the protection against side-channel attack is possible in principle. In order to ensure that the PQC schemes to be used are secure against quantum attacks, more rigorous testing is needed. This entails rigorously studying the security of PQC schemes against both quantum and classical attacks.
The second major challenge is that all the PQC schemes are bulkier and slower to implement than the existing schemes. The key sizes of all the schemes are roughly ten-times or larger than the existing key size used in ECC. Moreover, the computational cost associated with key generation and authentication of the NIST-approved PQC schemes are substantially more demanding.
Therefore, if we simply swap out the ECC by one of the NIST-approved PQC schemes, there will be a substantial overhead on the blockchain network, leading to slower and more expensive transactions. Can we build a PQC scheme which is as lean as ECC while being resistant against quantum attacks? It is far from clear if this is possible, and substantial progress must be made to achieve this goal. This also means that there will be an ample amount of opportunities in this direction. Building/upgrading a blockchain to the extent that it is seamless with the current experience, while ensuring security against quantum attacks, will be a new opportunity to rebuild Web3.
5. Final Word
Quantum computing introduces a unique duality for the crypto space. On the one hand, it raises long-term questions around the resilience of existing cryptographic standards. On the other, it offers a technical horizon that could eventually enrich how blockchains operate — particularly in areas like randomness, computation, and protocol design.
While the hardware required to compromise ECC remains well beyond current capabilities, progress in quantum error correction and scaling continues steadily. The arrival of an intermediate-scale error-corrected quantum computer (ISEQ) would be a strong signal that the threat is moving from theoretical to practical — and would likely prompt more serious conversations around protocol upgrades.
In the meantime, there is no need for panic or cause FUD, but there is a strong case for preparation. Post-quantum schemes are improving, and the industry has the time and space to experiment, test, and plan. It is not possible to accurately predict the timing of developments in the quantum computing sector, but industry leaders in crypto should work together with their QC counterparts early to ensure that those developments are quantum opportunities rather than quantum threats.
Appendix: Definitions
Coherence Time
The duration over which a qubit can retain its quantum state (superposition or entanglement) before it decoheres due to environmental noise or internal imperfections. A longer coherence time enables more quantum operations (gates) before errors become significant, and is critical for meaningful quantum computation.
DARPA QBI / US2QC
US government-led programmes: QBI (Quantum Benchmarking Initiative) aims to establish fair performance metrics for quantum systems, while US2QC (Underexplored Systems for Utility-Scale Quantum Computing) funds novel, scalable architectures that could reach practical quantum advantage beyond NISQ-era limitations.
Discrete Logarithm
The problem of determining the exponent in the equation gx≡hmod pg^x \equiv h \mod p, which is considered computationally hard. It forms the cryptographic foundation for many public-key systems, including Diffie–Hellman and elliptic curve cryptography, but is vulnerable to quantum attacks like Shor’s algorithm.
Elliptic Curve Cryptography (ECC)
A public-key cryptosystem that uses the algebraic structure of elliptic curves over finite fields to offer high security with small key sizes. Efficient and widely adopted, ECC is considered vulnerable to quantum attacks, particularly Shor’s algorithm, which could break it in polynomial time.
Entanglement
A uniquely quantum mechanical property where two or more qubits are linked such that the state of one immediately affects the state of the other(s), regardless of distance. Entanglement is essential for quantum teleportation, superdense coding, and many quantum algorithms.
Error Correction
The process of detecting and correcting errors in quantum states without directly measuring the qubit. It involves encoding logical qubits using multiple physical qubits to protect against bit-flip, phase-flip, and more complex noise, essential for building fault-tolerant quantum computers.
Fault Tolerance
The capability of a quantum computer to perform reliable computations despite hardware faults or qubit errors, typically achieved through layered error correction codes and system-level redundancy. It’s necessary for scalable, long-duration quantum computation.
Gate-Based Quantum Computing
A quantum computing model where computations are executed via sequences of quantum logic gates applied to qubits, analogous to Boolean gates in classical circuits. Most general-purpose quantum computers under development (e.g., by IBM, Google) follow this paradigm.
Grover's Algorithm
A quantum search algorithm that provides a quadratic speed-up over classical brute-force methods. It finds an item in an unstructured database of N items in O(√N) steps, and threatens symmetric key cryptography by reducing effective key length.
Hashed Public Key
A cryptographic technique where a public key is passed through a hash function, producing a shorter and often more private identifier. Used in blockchain systems to enhance privacy (e.g. Bitcoin addresses) and reduce key size in post-quantum settings.
Host Processor
The classical computing unit that manages the execution flow, error correction, and interfacing between users and the quantum processor. It coordinates quantum instructions and post-processes measurement outcomes in hybrid quantum-classical systems.
Interference
A fundamental quantum effect where the probability amplitudes of different computational paths combine—constructively or destructively—enabling quantum algorithms to amplify correct answers and suppress incorrect ones, unlike classical probabilistic computation.
ISEQ (Intermediate-Scale Error-Corrected Quantum Computer)
A proposed class of quantum computers that bridges the gap between noisy intermediate-scale quantum (NISQ) devices and fully fault-tolerant machines. ISEQ systems incorporate some level of error correction, enabling more reliable execution of useful algorithms.
Lamport Signatures
One of the earliest forms of one-time signature schemes, relying only on hash functions for security. Lamport signatures are quantum-resistant and serve as a basis for many hash-based post-quantum cryptographic systems.
Logical Error Rate
The probability that an error occurs in a logical qubit (which is error-corrected) rather than an individual physical qubit. Lower logical error rates indicate effective error correction and are a critical benchmark for practical quantum computation.
Logical Qubit
A qubit that represents encoded quantum information protected by error correction across multiple physical qubits. Logical qubits behave like ideal qubits, even in the presence of noise, and are essential for fault-tolerant quantum computing.
Measurement Collapse
The act of measuring a quantum state forces it into a definite classical outcome (e.g., 0 or 1), destroying any superposition or entanglement. This collapse is irreversible and central to how quantum systems yield usable results.
Neutral Atoms
Atoms with no net electric charge used as qubits in certain quantum computing architectures. They are trapped and manipulated using optical tweezers and offer promising scalability and coherence for large-scale quantum systems.
One-Time Signature (OTS)
A digital signature scheme designed for single-use, where each key pair signs exactly one message. OTS schemes, such as Lamport or Winternitz, are simple and post-quantum secure, making them useful in hybrid or layered cryptographic protocols.
Photons / Photonic Qubits
Qubits represented by photons, the quantum particles of light. Photonic qubits are ideal for communication and networking due to their speed and low noise, and are used in quantum key distribution and linear optics quantum computing.
Physical Qubit
A single hardware-based qubit that encodes quantum information, subject to errors from environmental noise. Multiple physical qubits are typically combined to form a more stable logical qubit.
Post-Quantum Cryptography (PQC)
A branch of cryptography focused on developing secure algorithms resistant to quantum attacks, often based on hard lattice problems, hash functions, or code theory, to replace vulnerable schemes like RSA and ECC.
Public-Key Cryptography
An encryption system using two mathematically related keys: a public key for encryption and a private key for decryption or signing. It underpins secure communication and digital identity but faces existential threats from quantum computing.
Qubit
The fundamental unit of quantum information, which can exist in a superposition of the classical 0 and 1 states. Qubits enable parallelism and entanglement, powering the advantages of quantum computing over classical systems.
Qubit Decoherence
The process by which a qubit loses its quantum properties due to environmental interference, resulting in classical behaviour. Decoherence limits quantum computation time and necessitates error correction.
Quantum
Pertaining to the smallest, indivisible units of physical properties like energy or information, governed by the laws of quantum mechanics. In computing, it enables radically different paradigms from classical logic.
Quantum Annealing
A heuristic quantum computing method that uses quantum tunnelling and adiabatic evolution to find low-energy (optimised) solutions to combinatorial problems. It’s particularly effective for certain optimisation and machine learning tasks.
Quantum Control Plane
The subsystem of a quantum processor that manages the timing, synchronisation, and fine-tuned control signals (e.g. microwave pulses) for executing gate operations on qubits.
Quantum Data Plane
The component of a quantum computing system responsible for carrying out the actual quantum operations, including qubit state preparation, manipulation, and measurement.
Quantum Error Correction
A suite of techniques to preserve quantum information against errors from decoherence, gate faults, or measurement disturbances. It encodes logical qubits across redundant physical qubits to detect and fix issues without collapsing the state.
Quantum Fourier Transform (QFT)
A quantum analogue of the classical discrete Fourier transform, used in many quantum algorithms such as Shor’s for period finding. QFT is exponentially faster than classical DFT for certain applications.
Quantum Random Beacons
Devices or services that use quantum processes to generate unpredictable, verifiable random values. These are useful for lotteries, leader selection, and cryptographic randomness where unpredictability is essential.
Quantum-Enhanced MPC
Secure multi-party computation protocols that integrate quantum capabilities—like entanglement or quantum communication—to improve security, efficiency, or correctness over classical-only methods.
RSA
A classical public-key cryptosystem based on the difficulty of factoring large integers. RSA is widely used but highly vulnerable to quantum attacks, particularly Shor’s algorithm, which can break it efficiently.
Shor's Algorithm
A quantum algorithm that factors large integers in polynomial time, breaking the security of classical cryptographic schemes like RSA and ECC, and motivating the need for post-quantum cryptography.
Side-Channel Attack
An attack method that extracts cryptographic keys or secrets by analysing information leaked through physical implementation details—like power usage or timing—rather than breaking the underlying algorithm.
Superconducting
Describes materials that exhibit zero electrical resistance at very low temperatures, enabling highly coherent qubit designs used in leading quantum hardware platforms like those from IBM and Google.
Supersingular Isogeny
A post-quantum cryptographic technique based on finding paths (isogenies) between supersingular elliptic curves. It offers potential resistance to quantum attacks and compact key sizes for secure communications.
Superposition
The quantum property that allows a qubit to exist in a blend of both 0 and 1 simultaneously, enabling massive parallelism in computation not possible in classical systems.
Topological Qubits
A proposed form of qubit that stores information in the topological properties of particles, making them inherently resistant to local noise and error. They are still largely experimental but offer strong fault-tolerant potential.
Trapped Ions
A quantum computing approach where individual ions are confined in electromagnetic fields and manipulated with lasers. Trapped ions exhibit long coherence times and high-fidelity gates, making them a strong candidate for scalable systems.
Winternitz Scheme
An optimisation of the Lamport one-time signature that balances signature size and speed by allowing limited multiple-use hash chains. It’s part of the design space for practical post-quantum signature systems.




